Cinemática Vetorial
SOMA DE VETORES

a) Vetores de mesma direção e sentido.
Dados:
│V1│ = 10
│V2│ = 8
Temos dois métodos para efetuar a soma:
Método algébrico e Método gráfico
Método algébrico
S = 10 + 8
│ S │ = 18
SOMA DE VETORES
b) Vetores de mesma direção e sentidos
opostos.
Dados:
│V1│ = 10
│V2│ = 6
Método algébrico
S = 10 + (- 6 )
│ S │ = 4
S = V1 + V2
ATENÇÃO:
O vetor soma S ( ou vetor Resultante R ) apresenta o mesmo sentido do vetor de maior módulo.
VETOR OPOSTO
Dado o vetor V , chamaremos de vetor oposto de V, o vetor -V que tem a sua representação indicando a mesma direção, mas com o sentido oposto. Veja a representação de - V.
SOMA DE VÁRIOS VETORES
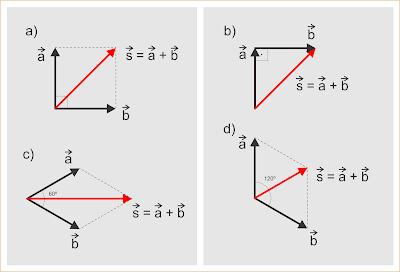
A soma de n vetores poderá ser feita através do método do polígono fechado. Veja o exemplo abaixo:
PRODUTO DE UM NÚMERO REAL POR UM VETOR
Chama-se produto de um número real n pelo vetor V ao vetor: p = n . V de tal maneira que:
1o ) módulo: │ p │ = │n│ . │ V │
2o ) direção: a mesma de V
3o ) sentido: de V se n é positivo
contrário a V se n é negativo.
Se n = 0 o produto p é igual a zero, ou seja, o vetor p é um vetor nulo.
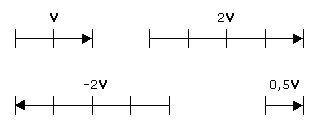

DECOMPOSIÇÃO DE VETORES
Um vetor V pode ser decomposto em dois vetores componentes: Vx (componente horizontal) e Vy (componente vertical), de modo que:

